10.What is Logic?
by Stephen Palmquist (stevepq@hkbu.edu.hk)
Today we begin the second of the four main parts of this course. In Part One the roots of the tree of philosophy provided us with an important insight about metaphysics, initially discovered by Socrates, but expressed in a far more complete form by Kant. Just as the roots of a tree are almost entirely buried in the soil so that we cannot see them as they are (at least, not without uprooting the tree), so also the metaphysical underpinnings of our knowledge consist of something essentially unknowable to the human mind. Armed with this insight, we can now extract ourselves from the murky depths of metaphysics and ascend to a part of the philosophical tree that allows itself to be seen more readily.
As we saw in Lecture 1, the trunk is to a tree as "logic" is to philosophy. But what is logic? In a moment, I would like you to share your answers to this question. My guess is that before you started this course most of you had more ideas about the nature of logic than about the nature of philosophy in general. So I hope this discussion question will be a bit easier than the one we had in the first lecture. Who would like to make the first suggestion? What is logic?
Student H. "I think logic is like science: it's supposed to teach us about the facts in the world, so we don't have to rely only on our own opinion."
Logic certainly does have something to do with helping us see beyond our own opinion. But I'm afraid I can't agree with you when you relate logic so closely to scientific facts. Nevertheless, I'm glad you spoke up, because this is a mistaken idea about logic that many beginning philosophy students have. Logic actually has nothing to do with teaching us new facts! In fact, it's more like metaphysics than physics when it comes to the issue of teaching us new facts. Metaphysics, at least for Kant, does not extend knowledge at all, but prevents errors, just as the roots of a tree do not bear fruit, yet need to be cared for in order to insure the fruit will be healthy. And the same is true for the trunk, logic. The reason for studying metaphysics and logic is not so we can know more, but rather so we can learn to express more clearly and accurately the knowledge we gain from other sources. Otherwise we might find ourselves cultivating insights that look good on the outside, but are rotten when we "bite into" them. So what is logic?
Student I. "Logic is step by step thinking, like the kind scientists always use."
I think you're right to suggest that scientific thinking must be logical. And "step by step" thinking, assuming the steps follow according to some definite order, is certainly one of the main characteristics of anything logical. The word "order" implies a definite relationship exists between the different steps we follow in our thinking. I assume that's what you mean by saying "step by step". But your answer shows that you have misunderstood my question. Can anyone see how? If a beginning history student asks me "What is history?", would it be adequate for me to answer him by saying "History is something important about the past"? Can any of you who are studying history right now tell me whether or not this accurately describes what you are learning about?
Student J. "We do learn a lot about significant events that happened in the past."
But is that all you learn about? Surely students in all subjects learn important things about the past without actually studying history. For example, in the last few lectures we've been learning about metaphysics by studying the ideas of past philosophers; but taking an historical approach does not mean we were studying history as such. What else have you been learning about in your history classes?
Student J. "Some teachers have presented different theories about how historical change actually takes place, such as the debates over whether history is like a line or a circle. Also, we are supposed to be learning not just facts about the past, but why they were significant, and how we can interpret them in the best way."
Very good! Now, just as all academic disciplines teach something about the past without necessarily teaching history, so also all academic disciplines are-or at least, should be-logical, yet do not teach logic. Not just science subjects, but history, economics, politics, religion, even music and art, are also normally taught in an orderly, logical way (though there are, of course, different types of order). So what I am asking you now is to tell me what makes logic itself different as an academic discipline? As we turn our attention to logic, what is it that we will be studying?
Student K. "The principles of orderly thinking?"
Yes! This could even be used as the basis for a general definition of logic. Logic as an academic discipline is distinguished from other disciplines by the fact that logicians do not simply use orderly thinking; they think in an orderly way about orderly thinking. Probably the most common definition for logic is to regard it as "the science of the laws of thinking".
This definition reminds me of a special term Kant had for describing the patterns built in to human reason. He compared good philosophers to architects who construct systems (conceptual "buildings") according to a predetermined plan. Reason's own "architectonic" structure provides a set of ready-made patterns that Kant believed philosophers should use as tools for presenting their philosophical ideas in a more orderly way. Kant himself never spent much time explaining just what these patterns are; but here in Part Two, quite a lot of our attention will be devoted to this task. As we shall see, it is through logic that we can best recognize an idea and an ordering of its parts, which Kant regarded as a prerequisite for understanding a philosophical system.
Of course, giving a simple definition of logic is not the only way of answering our question. Who else has an idea about what logic is?
Student L. "I remember in one of the first lectures you talked about the Greek word logos. Does that have anything to do with what we're supposed to be learning for the next few weeks?"
You probably also remember that, when I mentioned logos in the third lecture, I was trying to shed some light on the significance of myths for philosophy. The term logos can sometimes refer to the myth itself, or to some unknown, hidden meaning. However, I think it is best to interpret it as referring to the first attempt to express this meaning in words. Since "logos" means "word", we could say that in this sense the term "logical" refers to a use of words whereby the words carry some meaning. As we shall see in this week's lectures, there are two types of logic: one type virtually ignores any hidden (i.e., mythical) meanings, while the other type focuses almost entirely on bringing just such meanings out into the light.
Words generally carry a meaning when used in combination with other words. The special term used in logic to denote a sentence that puts forward a meaningful relation between two or more words is the term "proposition". For example, our discovery in Lecture 5 that for Aristotle "substance is form plus matter" could be regarded as a simple proposition, showing a definite relationship between three concepts: "substance", "form", and "matter". In the next lecture I shall introduce some special terms that will enable us to refer to the most important types of propositional relations by name.
Why is it important to learn how words get their meaning? If we know what a word means, why do we need to go further and learn the laws that determine how that meaning arises? This should be an easy question to answer, since I've already mentioned the reason at the beginning of today's session.
Student M. "If we don't know the rules, we might make errors without knowing it. Learning the rules will help us think and speak truthfully. A logical person can avoid saying anything that is false."
Avoiding errors is indeed the answer I was thinking of. But once again, we have to be careful not to think something we say is always true just because it is logical. It might surprise you to find out that logic is not really concerned about the truth of the words we use, but only about their truth value. As we shall see, it is possible to say something that is utterly false, yet to express it in a logically correct (or "valid") way, or to say something that is very true, but to state that truth in a logically incorrect way. The kind of errors logic helps us to avoid are not called "falsehoods", but "fallacies".
A fallacy is a mistake in the structure of the argument we use to draw a conclusion based on some evidence. The most important fallacy for you to learn is closely related to what can be called the problem of self-reference. Because I so frequently find students committing this fallacy in their insight papers, I'll warn you about its dangers here at the outset of our study of logic. The term "self-reference" refers to any proposition that refers to itself. Most such proposition entail no logical problem. For example, if the word "this" in the sentence "This sentence is true" refers to itself (i.e., to the sentence in quotes), we have no difficulty is understanding how it could be true. However, if we change the sentence just slightly, to read "This sentence is false", then a huge problem arises once we assume the word "this" refers to that sentence. The problem is that if the proposition has a positive truth value (i.e., if we want to claim it is true), then this requires us to believe the sentence is false, because that's what the sentence says about itself. Yet if we accept that the proposition is false, then (according to what the sentence tells us to believe) it must be false to say the sentence is false. That is, if it's true, it's false, and if it's false, it's true! This creates what is sometimes called a "vicious circle"-i.e., a never-ending cycle of implications that makes it impossible to determine the proposition's meaning.
In student insight papers this problem appears in a wide variety of disguises. One of the most common is in papers on topics such as "What is truth?" or "How do I know what is right and wrong to do?" or "What is the standard of beauty?" Typically, students will take note of the fact that different cultures (and sometimes even different people within the same culture) have different views on such questions. They will then conclude: "there are no definite answers". But drawing such a conclusion is fallacious, because it fails the test of self-reference. This becomes clear once we recognize that this proposition is being used to provide a definite answer to the question at hand-i.e., an answer that will end the discussion (as all genuinely definite answers do) by insisting that the search for a definite answer is a dead-end search. Since "there are no definite answers" is itself a definite answer, the sentence itself provides a counter-example of what it is claiming to be true: if it is definitely true to say "there are no definite answers", then the same proposition must be false, because it illustrates that there must be at least one definite answer!
This fallacy can be corrected in two ways. First, we can recognize that the proposition in question is an exception to the rule. In this case, we are essentially admitting the presence of a myth. That is, a person can say: "The only definite answer to this question is that there are no definite answers (other than this one)." To do so is to affirm a myth; but the problem of self-reference illustrates that we can never do away completely with all myths. Sometimes it is better simply to become aware of our myths (our indefensible presuppositions), rather than to pretend that we have none at all. A second option would be to express the conclusion in a more accurate and meaningful way, such as: "there are too many definite answers". This fits the kind of evidence typically provided in such insight papers, where the preceding argument has compared several competing definite answers to whatever question is being considered. Indeed, most (if not all) philosophical questions have this important characteristic. They are not questions that have no answer, otherwise it would be pointless to discuss them. Rather, they are questions whose multitude of potentially good answers leaves us unable to say for certain which answer is best. Of course, this second option is not independent of the first, because we are actually saying: "The best answer is that there are many good answers, but no best answer (other than this one)."
Learning to identify this and the many other types of fallacies can be a very useful skill, though you needn't bother to learn the fancy Latin names they are often given. Some common fallacies to watch out for when writing your insight papers are: arguing ad hoc (from a single example), ad antiquitatem (from tradition), ad novitatem (from newness), ad baculum (by appealing to force), or ad hominem (appealing to a personal weakness of the opponent or of others who accept the same conclusion); shifting the "burden of proof" (i.e., claiming your view is justified as long as nobody proves it is wrong); equivocation (i.e., using a word in two different ways without pointing out the difference); arguing against a "straw man" (i.e., a weak, easily refuted version of the opponent's view); "begging the question" by assuming what you want to prove-and the list goes on almost without an end. However, some philosophers are so fond of labeling any and every type of logical error as a fallacy that their search for fallacies becomes a fallacy of its own. This happens whenever a person assumes that locating a fallacy in an argument is a sufficient reason to treat the argument's conclusion as either false or meaningless, and therefore refuses to consider it any further. To treat fallacies in this way is to commit what I call (intentionally playing around with a bit of self-reference) the "fallacy fallacy"! That is, it is a fallacy to infer from the fact that an argument contains a fallacy that its conclusion must be untrue.
Let me illustrate this point with a simple example. If I say "History and philosophy have nothing in common with each other; you are an historian and I am a philosopher; therefore we have no common interests", then my argument is fallacious. Even if the first two statements (called "premises") are both true, they do not necessarily imply the third statement, because you and I might have something in common that has nothing to do with history or philosophy. On the other hand, even if one or both premises were false, the conclusion might be true: history and philosophy might be closely related in certain respects, or you might be studying chemistry, not history; but we might have no common interests. Logic on its own is incapable of telling us whether or not either of these two scenarios is factually true; all it can do is tell us under what conditions the truth of a specific claim can be demonstrated to be true. It would therefore be a fallacy to assume that because my argument contains a fallacy, it's conclusion is necessarily untrue.
Logicians sometimes make this point by saying logic is concerned with "formal truth" rather than "material truth". The material truth of a proposition is the particular external fact that makes the proposition true or false. Thus, if we want to demonstrate the material truth of the statement, "This chalk is white", the best way is for me simply to hold it up like this, so you can all see that it is white. The proposition is true if it turns out that the chalk in my hand really is white. The formal truth of a proposition, by contrast, is the general internal way it is expressed. By "internal" I mean that, without going outside of the proposition itself, we can determine its formal truth value. As an example let's take the complex proposition, "If this chalk is completely white, then it is not blue." In this case, we can say that, without looking at the chalk at all, we know that if the first part of the proposition is true, then so is the second.
A proposition's formal truth does not depend at all on the specific meanings of the words used within the proposition. All that matters is that we know the truth value of each of its parts. For that reason, logicians often find it is helpful to substitute the words in a proposition with symbols. Because the symbols represent only the general or formal properties of each word, they make it easier to look beyond the particular content and see the proposition's underlying logical structure. Thus, the ideal goal of some logicians is to develop a complete symbolic logic that can function, rather ironically, as a language without words (i.e., logic without logoi). For example, the above "If ... then ..." proposition can be expressed by replacing "this chalk" with "a", "all white" with "w", "not" with "-", and "blue" with "-w" (i.e., "not white"), so that the formal structure of the proposition becomes clear: "If a is w, then a is -(-w)" is always a true proposition, no matter what words we use to replace these symbols.
The proliferation of symbols in logic texts is, perhaps more than anything else, what scares beginning philosophy students away from logic. But like any new language, once we learn how to use these symbols, the initial awkwardness and confusion goes away. In this course I shall introduce only a very small number of logical symbols to you. But judging from your insightful suggestions regarding the nature of logic, I am hopeful that some of you will be interested enough to do further reading on your own in the area of symbolic logic. My main interest in the next eight lectures will be to help you deepen your insight into what logic itself actually is.
11. Two Kinds of Logic
I shall begin this lecture by looking at a typical example of how logic can help us see the formal relations between words and the truth value of the proposition they compose. A proposition's truth value, as I explained in the last session, is quite distinct from its actual, material truth. It refers to the truth or falsity a proposition would have under any given set of conditions. Thus, we can find the truth value of a proposition without knowing anything at all about its actual content, provided we know what kind of proposition it is. One way of doing this is to construct what is called a "truth table" for the proposition. Let's take as an example the proposition: "If you read the textbook, then you will do well on the final exam." (Actually, I would prefer not to give written exams-or any grades, for that matter-since it is nearly impossible to judge how much real philosophy you have learned just by administering a conventional test. The purpose of this course is not to teach you about philosophy-that can be tested quite easily-but to teach you to philosophize. Nevertheless, universities require teachers to "grade" their students, so let's use logic to remind ourselves of one good way to make that grade a high one, if you are reading this as part of a graded course.)
The first step in constructing a truth table is to reduce the proposition in question to its simplest logical form. In this case we can replace "you read the textbook" with p and "you will do well on the final exam" with q, giving us the proposition "If p, then q". This can be expressed entirely in symbols as "p?/span>q", where the arrow means "implies" (this being logically equivalent to "If ..., then ..."). The second step is to substitute for each variable all the possible combinations of "T" ("is true") and "F" ("is false"), and determine for each combination whether the resulting proposition is true or false. The appropriate letter (T or F) is then written in the far right column, as in Figure IV.1a. If it is true that "you do the readings", then, as the truth table tells us, the proposition will be true only if you pass the exam. If, on the contrary, the p statement is false, then the proposition will be logically true regardless of the truth or falsity of q. The reason for this rather surprising result can be seen more clearly if we convert the proposition into its equivalent "Either ..., or ..." proposition. If p really does imply q, then either q is true or p is false. Since p's truth implies q's truth, the falsity of q would imply the falsity of p. That means "p ?q" is equivalent to "-p ⁄ q" (i.e., "Either -p, or q"). Constructing a new truth table, as in
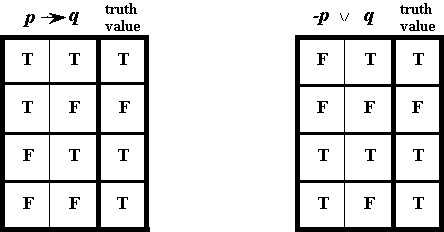
(a) "If ..., then ..." (b) "Either ..., or ..."
Figure IV.1: Two Truth Tables
Figure IV.1b, we now find that the second row is the only one in which both choices are false; each of the other three propositions has at least one true option, so that the overall proposition can be judged to be true. (Note that the first column in Figure IV.1a contains the opposite values as those in Figure IV.1b, because the former is a function of p, while the latter is a function of -p.)
Being aware of the truth value of various types of proposition can help us avoid being fooled by arguments that attempt to prove something by presupposing a false p. Since the whole proposition is formally true regardless of the truth or falsity of q, we can use such an argument to "prove" the truth of something that is actually false. For example, if I want to make myself appear to be your favorite teacher, I could argue: "If you are the Chief Executive of Hong Kong SAR, then I am your favorite teacher!" Since the premise is false (because none of you is the Chief Executive), this proposition is true whether or not I am actually your favorite teacher! For it is the same as saying "Either you are not the Chief Executive of Hong Kong SAR, or I am your favorite teacher." So when faced with a proposition that has a false p, always be sure to remember that it is a fallacy to conclude from the truth value of the whole proposition that the q is actually true.
Now let's imagine that you do the recommended readings for this class, but you end up failing the exam anyway. If the proposition whose form is analyzed in Figure IV.1a were actually true, then you could come and argue from logic alone that you should pass the class. For example, you could remind me that the proposition I stated at the beginning of today's class is equivalent to another proposition: "Either you did not do the readings, or you passed the exam." The truth value of this proposition, as shown in Figure IV.1b, requires that in order for it to be true, at least one of its two parts must be true. So if p ("you did not do the readings") is false, and if my original proposition is true, then as the truth table shows, q ("you passed the exam") must be true. So don't ever say logic is too abstract to have any practical value!
Such tables can, in principle, be constructed for any proposition, though they would become quite cumbersome for propositions with many discrete components. For our purposes, these simple examples will suffice. In the next few lectures we will meet some patterns that are rather similar to those used in such truth tables. But for the rest of this lecture I want to focus on what I believe is the single most important distinction in logic: namely, the distinction between "analysis" and "synthesis". Rather than giving a universal definition of these two terms, I shall explain how they can be applied to make three key distinctions: namely, distinctions between methods of argumentation, types of proposition, and kinds of logic.
The distinction between analytic and synthetic methods of argumentation is more commonly known as the distinction between "deduction" and "induction". A deduction is an argument that starts by positing two or more propositions, called "premises", presupposing them to be true. A conclusion is then drawn that is supposed to follow necessarily from the premises. The archetypes of all deductions are those with three steps, called "syllogisms". And the most common one of all is the "categorical" syllogism. The standard example of this type of syllogism is the one Socrates used to persuade his friends not to worry about his impending death, inasmuch as death is inevitable. It looks like this:
All human beings are mortal.
Socrates is a human being.
\ Socrates is mortal. (The symbol "\" stands for "therefore".)
In this case the first proposition (or "major premise") puts forward a universal assumption; the second proposition (or "minor premise") puts forward a particular test case; and the third proposition, of course, draws a necessary ("categorical") conclusion, also called the "inference". The only way the conclusion could prove to be false would be if one of the two premises is false, unless of course the formal relations between the terms in these propositions are in some way fallacious.
A good way to test whether or not the terms in a deduction contain a fallacy is to convert the propositions into a set of corresponding logical symbols. In the example given above, commonly known as "universal implication" (because of the use of the word "all"), the words are typically converted into symbols such as the following:
All h's are m.
S is an h.
\ S is m.
As far as formal logic is concerned, the validity of this syllogism remains exactly the same, whether "h" refers to humans or horses, whether "m" refers to being mortal or to being moral, and whether "S" refers to Socrates or Santa Claus! But remember: proving an argument to be valid still leaves open the question of whether the premises are actually true. (The other words, "all", "are", etc., can also be converted into symbols-but I don't want to scare you away from logic at this early stage!)
Another important aid for anyone who wishes to explore the formal structure of any deductive argument was provided more than two thousand years ago, by Aristotle, the founder of formal logic. He developed a virtually complete system of all the possible forms of deductive argument. Until the beginning of the twentieth century, virtually all philosophers regarded this system as giving an unsurpassable account of all the basic propositions of formal logic. This, without a doubt, gives Aristotle the honor of introducing the single most universally recognized and longest-lasting contribution ever made to philosophy. However, for our purposes it is not necessary to learn all the details of Aristotle's system, especially since his ideas were superseded in numerous respects during the past one hundred years.
What is more significant here is that deduction is not the only respectable form of philosophical argument. For this analytic method is complemented by an equally significant synthetic method. This method, called induction, requires us to begin by appealing to various material facts which, taken together, point to the desired conclusion. That is, in contrast to the necessity governing a valid deduction, induction always involves some guesswork. Or, to borrow from Kant's terminology (see Lecture 7), we could say deduction remains entirely within the realm of concepts, while induction requires an appeal to intuitions as well. Perhaps an example will help to illuminate this difference.
Let's say we want to prove that the proposition "The sun always rises in the east" is true. In order to deduce the truth of this statement, we would need to find at least two true assumptions which, taken together, necessitate such a conclusion. For example, we might choose the following:
All planets revolve around a star in such a way that the star always appears to rise on the planet's eastern horizon.
The earth is a planet and the sun is a star.
\ The sun always rises in the east.
In order to arrive at this same conclusion by induction, on the other hand, we would need to argue in something like the following way:
My father says the first day he saw the sun rise, it rose in the east.
My mother says the sun rose in the east on the day I was born.
The first day I remember seeing the sun rise, it rose in the east.
Last week I woke up early and saw the sun rising in the east.
Yesterday I did the same thing.
I have never heard anyone say they have seen the sun rise in the north, south, or west.
\ The sun always rises in the east.
In Lecture 21 we shall raise the question whether we are ever capable of reaching a necessary truth by induction. But for now I am only trying to illustrate the difference between it and deduction.
The terms "analysis" and "synthesis", as labels for distinguishing deductive and inductive methods of argumentation, are at least as old as Euclid. In his Elements, Euclid made it abundantly clear that these two methods should not be seen as mutually exclusive, but as complementary. His method was to demonstrate the correctness of each of his geometrical theorems by first using an analytic (deductive) method of argumentation, and then supporting its conclusion with synthetic (inductive) reasoning. Following his lead, we can picture the opposing "directions" entailed by these two methods as arrows pointing opposite ways:

(a) Deduction (b) Induction
Figure IV.2: Two Methods of Argumentation
Whereas the actual process of constructing a deduction (as opposed to its written form) starts by formulating a conclusion, then proves it by searching for two or more true assumptions that can serve as its basis, the process of induction starts by collecting innumerable bits of evidence, then using them as the basis to draw a conclusion.
As I mentioned earlier, the terms "analytic" and "synthetic" have been used in several quite different ways by philosophers. For a long time Euclid's way of using the terms, to refer to two methods of argumentation, was the commonly accepted usage. But Kant developed a new way of using the same terms, whereby they refer to two distinct types of proposition. According to Kant, a proposition is analytic if the subject is "contained in" the predicate, whereas it is synthetic if the subject goes "outside" the predicate. Thus, for example, "Red is a color" is analytic, because the concept "red" is already included as one of the constituents of the concept "color". Likewise, "This chalk is white" is synthetic, because you would not know that this thing I'm holding in my hand is chalk if I merely told you it is white. Using these two examples, we can picture Kant's initial description of this distinction in terms of the two maps shown in Figure IV.3.
Kant also gave several other, more rigorous, guidelines for determining whether a proposition is analytic or synthetic. The truth of an
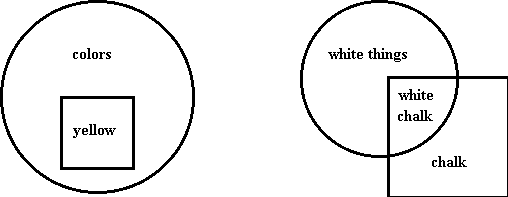
(a) "Yellow is a color." (b) "This chalk is white."
Figure IV.3: Analytic and Synthetic Propositions
analytic proposition can always be known through logic alone; so, if the meanings of the words are already known, the proposition is not informative. An analytic proposition is self-explanatory. All I have to do is say "white" and any of you who understand the meaning of this word will already know I'm talking about a color. So, like the conclusion of a good deduction, the truth of an analytic proposition is purely conceptual, and therefore, necessary. The truth of a synthetic proposition, by contrast, requires an appeal to something more than mere concepts. Like an inductive argument, an appeal will be made to some intuition-i.e., to some factual state of affairs. As a result, synthetic propositions are always informative, and the truth of their conclusions is contingent on a given state of affairs continuing to exist. When I tell you this piece of chalk hidden in the palm of my hand is white, the truth of my statement depends on whether or not I have somehow fooled you by slipping it into my pocket, or by replacing it with a blue piece of chalk, etc.
I hope you will try out a few of your own sample propositions to test your grasp of this distinction between analytic and synthetic propositions. Some philosophers nowadays think so many propositions are difficult to pin down as either analytic or synthetic that the whole distinction is worthless. However, I believe such "gray areas" cause problems only when we forget to look at the context of a proposition, or when we forget to apply each of Kant's guidelines with sufficient care. In any case, this is not an issue we can resolve in an introductory course such as this.
Instead, I'll just mention here that Kant combined this distinction between analytic and synthetic propositions (or "judgments", as he also referred to them) with another distinction, between "a priori" and "a posteriori" kinds of knowledge. "A priori" refers to something that can be known to be true without appealing to experience; by contrast, something is "a posteriori" if a demonstration of its truth requires an appeal to experience. This gives rise to four possible kinds of knowledge, two of which are non-controversial: analytic a priori knowledge is simply logical knowledge, and synthetic a posteriori knowledge is simply empirical knowledge. Kant believed there is no analytic a posteriori knowledge; I contend, however, that this term actually defines a very important, though often neglected, epistemological category. I've defended this contention at length elsewhere (see APK and KSP 129-140), so here I'll simply assert that classifying our hypothetical beliefs about the world in this way can do the crucial work of saving the appearances, both from being proudly mistaken for ultimate reality and from being discarded as mere appearances. The synthetic a priori class of knowledge occupied most of Kant's attention; for he argued that all transcendental knowledge is of this type. This is why he said the question "How are synthetic judgments a priori possible?" is the central question of all Critical philosophy. Although we won't have time to discuss the intricacies of these different logical classifications, you should make an effort to learn their interrelationships, as shown in the following map:
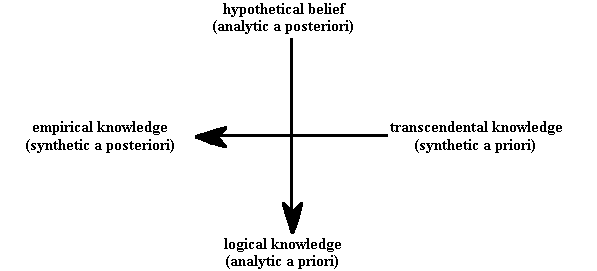
Figure IV.4: Four Perspectives on Knowledge
I would like to end today by introducing a third way of using the terms "analytic" and "synthetic". You won't find this use of these terms in any logic textbook, as far as I know. But it makes a useful addition to the way they have been used in the past. I find it very helpful to use these terms to distinguish between two distinct kinds of logic. "Analytic logic" is the entire body of logic based on the principles of reasoning set forth by Aristotle. The most basic of all these principles is what is often called the "law of contradiction". However, for reasons that will become clear later, I suggest we call it the "law of noncontradiction", especially since this principle tells us how we can avoid contradicting ourselves. Aristotle states this law in Categories by saying a thing cannot both be and not be in the same respect at the same time. In other words, it is impossible for a thing to be both black and white, both "A" and "-A", etc. The simplest symbolic expression of this law is:
"A is not -A" or "A≠-A"
It would be difficult to overstate the profound influence this law has had on the past two thousand three hundred years of philosophy. For upon it is based nearly all of the arguments western philosophers have put forward. Moreover, we would not be able to communicate with each other without assuming that when we use a word, we want those who hear us to think of the thing that word refers to, and not its opposite!
Deduction and analytic propositions are two aspects of analytic logic. In both cases, as we have seen, they are paired with complementary, synthetic functions: induction and synthetic propositions. This raises a very important question: Is there also a complementary form of logic itself, equal and opposite to analytic logic, out of which these (and other) non-analytic logical functions arise? And if so, is there a law governing this alternative logic? I'd like you all to think through these two questions on your own between now and the next time we meet. Then I shall begin the next lecture by offering an answer to these questions.
12. Synthetic Logic
At the end of the previous lecture I asked you to go away and think about two questions: What should we call the opposite of traditional, "analytic" logic? and On what law would such logic be based? Any of you who have read the lecture outline for this course (see above, p.vii) will have easily guessed that the term I think best describes the kind of logic governing functions like induction and synthetic propositions is "synthetic logic". But you may have had a bit more trouble thinking of a law to set alongside Aristotle's "law of noncontradiction". So let's begin today by determining what such a law would be.
Finding the basic law of synthetic logic need not be a difficult task. Analytic and synthetic logic always function in opposite ways, so all we have to do is determine the opposite of Aristotle's famous "A≠-A". There are two ways of doing this. We can either change the "≠" to "=" or change the "-A" to "A". In this way, we derive the following two laws:
"A=-A" and "A≠A"
I suggest we call the first new law the "law of contradiction", since it shows us the inherently contradictory form followed by anything that functions in a "synthetic" way. The second is actually the opposite of a rather boring law of analytic logic, usually called the "law of identity" (A=A); so we can refer to "A≠A" as the "law of nonidentity". This gives us a complete set of four basic laws of logic:
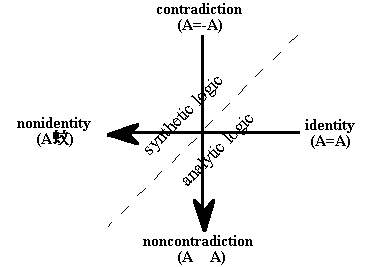
Figure IV.5: The Four Fundamental Laws of Logic
Obviously, the laws of synthetic logic require some explanation. For how could contradiction or even nonidentity be the basis for constructing any meaningful proposition? A computer, for example, could never work if it were programmed using synthetic logic rather than analytic logic. To attempt this would be like trying to operate the computer while it is submerged in water: the whole thing would short-circuit! What then is the point of talking about synthetic logic at all? What sense could it ever make to say, for instance, "Black is not black"? Fortunately, in spite of the tremendous advances we saw in computer technology during the 1990s, human thinking still surpasses that of the best computer. For, although even a small computer can out-think the most highly developed human brain in analytic operations, computers are incapable of performing genuinely synthetic operations. In order to see how synthetic logic can have meaningful applications, let's look at some examples.
Next to Confucius, one of the most influential ancient Chinese philosophers was Chuang Tzu (c.369-c.286 B.C.). As far as we know, he didn't write much; but what he did write is well preserved in a collection of thirty-three short essays. One of the most interesting of these utilizes synthetic logic on virtually every page. Even the title, "Discussion on Making All Things Equal", suggests that one of Chuang Tzu's main goals was to encourage us to break out of our ordinary, "black and white" way of thinking, by giving us a glimpse of what the world looks like if we learn to synthesize ("make equal") all such opposites. One passage in particular is worth quoting at length:
Everything has its "that", everything has its "this". From the point of view of "that" you cannot see it, but through understanding you can know it. So I say, "that" comes out of "this" and "this" depends on "that"-which is to say that "this" and "that" give birth to each other. But where there is birth there must be death; where there is death there must be birth. Where there is acceptability there must be unacceptability. Where there is recognition of right there must be recognition of wrong; where there is recognition of wrong there must be recognition of right. (CTBW 34-35)
So far, Chuang Tzu has merely pointed out the universal need of human beings to think analytically. He notes, quite rightly, that in such cases, the opposites actually depend on each other for their existence. But he then continues:
Therefore the sage does not proceed in such a way, but illuminates all in the light of heaven. He too recognizes a "this", but a "this" which is also a "that", a "that" which is also a "this". His "that" has both a right and a wrong in it; his "this" too has both a right and a wrong in it. So, in fact, does he still have a "this" and a "that"? Or does he in fact no longer have a "this" and a "that"? A state in which "this" and "that" no longer find their opposites is called the hinge of the Way [i.e., of the Tao]. When the hinge is fitted into the socket, it can respond endlessly. Its right then is a single endlessness and its wrong too is a single endlessness. So I say, the best thing to use is clarity. (CTBW 35)
Here Chuang Tzu explains that the way of the sage is to follow the Tao (the "Way" of heaven), and that this Way can be expressed in words only by using the contradictory language of synthesized opposites: "this" and "that" (Chuang Tzu's equivalent of "A" and "-A") must be identified with each other; moreover, each must be regarded as itself containing what we would normally regard as a contradiction: e.g., both right and wrong; both birth and death, etc.
Do you think Chuang Tzu was being serious when he wrote this, or did he intend it all to be a joke? Why did he end this rather confusing paragraph by stressing the need for clarity? Later (CTBW 37-38) he says: "The torch of chaos and doubt ... is what the sage steers by.... This is what it means to use clarity." He then announces he will "make a statement" that "fits into some category", though he's not sure which. What follows is a series of blatant contradictions, such as: "There is nothing in the world bigger than the tip of an autumn hair, and Mount T'ai is little. No one has lived longer than a dead child, and P'eng-tsu [the Chinese Methuselah] died young." Could he really have been aiming at clarity when he made such odd statements?
I don't think Chuang Tzu was joking at all-though the truth can often be funny. He reveals his intentions more fully when he says:
The Great Way is not named; Great Discriminations are not spoken; Great Benevolence is not benevolent; Great Modesty is not humble; Great Daring does not attack. If the Way is made clear, it is not the Way. If discriminations are put into words, they do not suffice.... (CTBW 39-40)
This suggests that the purpose of speaking in an intentionally unclear (or paradoxical) way is to point our hearts and minds beyond the realm of ordinary distinctions, where analytic logic suffices, to a deeper and far more important realm-to a reality that cannot be spoken about clearly and truthfully at the same time. In other words, Chuang Tzu taught that the obscurity of synthetic logic is the clearest way of expressing ourselves if we must use words to describe the indescribable. Life, real life, does not actually come in the neat little boxes that our minds create. Hence, an authentic life is one that sees beyond these artificial boundaries:
Right is not right; so is not so. If right were really right, it would differ so clearly from not right that there would be no need for argument. If so were really so, it would differ so clearly from not so that there would be no need for argument. Forget the years; forget distinctions. Leap into the boundless and make it your home! (CTBW 44)
Trying to force Chuang Tzu into the straight-jacket of analytic logic would leave us little choice but to declare him insane. However, once we recognize that his goal was to give us a glimpse of something beyond the boundaries of analytic logic, his words begin to take on a new kind of meaning. The "clarity" he recommended is not the clarity of thought (i.e., thinking about what we know), but the clarity of vision (i.e., seeing what remains mysterious). The irony is that he used words to point us to this vision. In so doing, he recognized that he was, in a sense, falsifying the true Way-at least, for anyone who focuses on his words as a literal description of his meaning, instead of focusing on what his words point to. And what we discover when we examine his words is that the tool he used most frequently to do the pointing is intentional contradiction. "Right is not right." What better example could there be of the law of nonidentity (A≠A) at work? "'This' is 'that'." What better example could there be of the law of contradiction (A=-A) at work?
Whereas analytic logic offers us the clarity of eyesight (i.e., thorough knowledge), synthetic logic offers us the clarity of insight (i.e., depth of understanding). When used properly, these two kinds of logic need not be viewed as competitors, but ought to be regarded as complementing each other, just as deduction and induction can be used effectively as complementary methods of argumentation. One of the best ways to picture their complementary relationship is to relate them to the distinction we learned from Kant, between the areas of possible knowledge and necessary ignorance, as in Figure IV.6. Analytic logic can be used to produce knowledge any time we are describing something that falls within the transcendental boundary (e.g., anything we can see). But once we use words to describe what lies beyond this boundary, analytic logic not only loses its explanatory power, but can actually mislead us into making false conclusions. Instead, as Chuang Tzu has shown us in describing the Tao, when dealing with issues that leave us necessarily ignorant, we can discover what to believe only by using synthetic logic to gain the insight needed to support such beliefs.
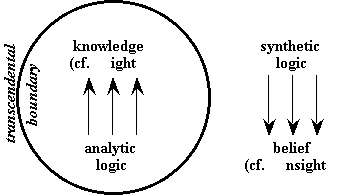
Figure IV.6: The Analytic and Synthetic Domains
It is no accident that Chuang Tzu regarded a "leap into the boundless" as the best way of understanding the truths of synthetic logic. This leap, sometimes called the "leap of faith", is essentially the leap from mere thinking about ultimate reality (as in academic metaphysics) to actually experiencing it. But "experience" here refers not to empirical knowledge, but to what Kant calls "intuition". For Kant, our power of intuition is a power of "receptivity", as opposed to "conception", which is a power of "spontaneity" (see CPR 92). So also, Chuang Tzu's "leap" is actually a leap into the Tao, into the intentional passivity of silence. This aspect of the "boundless" will be the focus of our attention in Part Four of this course. For now, it is enough to point out that analytic and synthetic logic provide us with two complementary perspectives: using the former, we actively impose onto the world strict conceptual divisions; using the latter, we passively receive from the world the power of its intuitive unity. Since this unity cannot be expressed literally in words, synthetic logic can be talked about only by viewing it as a parasite on analytic logic, based on the negation of the analytic laws. What other way would there be to express the inexpressible than to negate the laws of correct expression? In the absence of any alternative, synthetic logic could not completely destroy analytic logic without destroying itself! This is why good philosophers recognize both kinds of logic as legitimate philosophical perspectives and attempt to develop both as integral aspects of their philosophy.
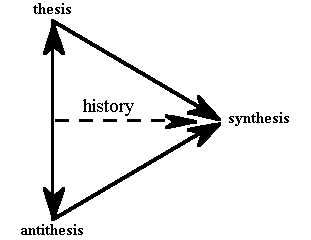
The western tradition has relatively few good examples of how synthetic logic can be employed to help us cope with our ignorance of ultimate reality. One ancient Greek philosopher, Heraclitus, touched upon synthetic logic with his insightful principle that "Opposites are the same" (i.e., "A=-A"). However, the little that remains of his writing does not provide much help as to how to apply this principle. Others have developed forms of synthetic logic into much more elaborate systems. The best example, undoubtedly, is Hegel (1770-1831), who constructed his entire "dialectical" philosophy on the principle that historical development
|
Figure IV.7: Hegel's Dialectical Method
|
takes place according to the synthetic pattern of "thesis", "antithesis", and "synthesis" (see Figure IV.7). This version of synthetic logic has had its greatest influence in this century in the form of "dialectical materialism"-the political ideology of Karl Marx (1818-1883), who, as we shall see in Week IX, turned Hegel's synthetic pattern upside down. Another interesting example comes fromThe Mystical Theology of a fourth century monk who used |
the pseudonym "Dionysius the Areopagite". Showing the futility of any attempt to describe ultimate reality (referred to as "It") he concludes:
Once more, ascending yet higher, we maintain that It is not soul or mind, or endowed with the faculty of imagination, conjecture, reason, or understanding; nor is It any act of reason or understanding; nor can It be described by the reason or perceived by the understanding, since It is not number or order or greatness or littleness or equality or inequality, and since It is not immovable nor in motion or at rest and has no power and is not power or light and does not live and is not life; nor is It personal essence or eternity or time; nor can It be grasped by the understanding, since It is not knowledge or truth; nor is It kingship or wisdom; nor is It one, nor is It unity, nor is It Godhead or Goodness...; nor is It any other thing such as we or any other being can have knowledge of; nor does It belong to the category of nonexistence or to that of existence; nor do existent beings know It as it actually is, nor does It know them as they actually are; nor can the reason attain to It to name It or to know It; nor is It darkness, nor is It light or error or truth; nor can any affirmation or negation apply to It ..., inasmuch as It transcends all affirmation by being the perfect and unique Cause of all things, and transcends all negation by the preeminence of Its simple and absolute nature-free from every limitation and beyond them all. (MT V)
This quotation reveals a profound awareness, long before Kant, of the fact that we can know virtually nothing about ultimate reality. Yet if we insist on interpreting these words according to the laws of analytic logic, then much of it appears to be nonsense! How, for example, can something be "not immovable nor in motion or at rest"? Such claims must be rejected as blatant contradictions, until we realize they are to be interpreted in terms of synthetic logic; for in so doing the same contradictions can point us toward deeper insights about the Being whom we normally call "God".
Although it is rare to find even a hint of the existence of synthetic logic in most logic textbooks, there have been a few scholars in this century who have recognized its significance and attempted to describe the way it works. No one to my knowledge has thoroughly explored to what extent it constitutes an entirely distinct kind of logic; yet some have openly acknowledged the possibility of using alternative laws as the basis for the way we use words. For instance, some anthropologists, in their study of how people in primitive societies think, have concluded that their minds operate according to what they sometimes call the "law of participation" (which means they see concepts as participating in their opposites). Other scholars have suggested still other names for what I have called the "law of contradiction", such as the "law of paradox". This name has the advantage of making it clear that the true purpose of synthetic logic is not to utter meaningless contradictions, but to drive our imagination to the point where it discovers new perspectives, from which the apparent contradictions can be resolved.
What we call this alternative kind of logic and its basic laws is not nearly as important as knowing how to use it. With this in mind, I'll discuss in Week V some very practical ways of using synthetic logic to gain insights. For today, let's conclude by reviewing what we have learned so far about logic, using the table given in Figure IV.8.
There are fundamentally two different types of logic: analytic logic arises out of the laws of identity and noncontradiction; synthetic
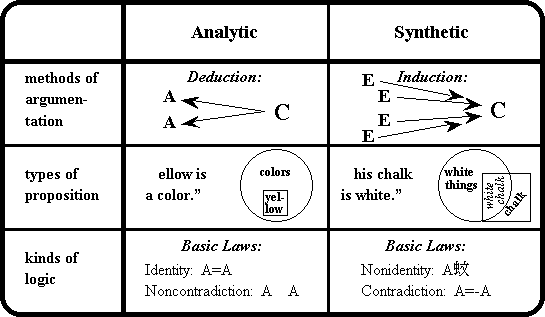
FigureIV.8:ThreeTypesofAnalytic-SyntheticDistinction
logic arises out of the opposite laws of nonidentity and contradiction. The former is properly used to describe anything that is possible for us to know; the latter is properly used to describe what, by its very nature, we can never know. Analytic propositions are an expression of analytic logic, because they identify two concepts that are already known to be, in some sense, identical; synthetic propositions are an expression of synthetic logic, because they identify two essentially nonidentical things-namely, a concept and an intuition. Finally, analytic logic is most appropriately manifested in the form of a deductive argument, where the conclusion follows from the premises as a matter of mathematical (i.e., noncontradictory) certainty; synthetic logic is most appropriately manifested in the form of an inductive argument, where the conclusion always depends on some degree of guesswork (i.e., on the paradoxical affirmation of what we do not know).
Having now introduced to you three of the most basic distinctions in logic, I shall devote next week's lectures to the task of explaining the logical basis of the various diagrams I have been using throughout this course. We will then conclude Part Two by looking at two examples from the twentieth century of philosophical schools that tended to over-emphasize analytic and synthetic logic, respectively, following by a third school that can be regarded as attempting to synthesize key aspects of the first two.
QUESTIONS FOR FURTHER THOUGHT/DIALOGUE
1. A. Is truth always true?
B. Is logic always logical?
2. A. Could there be an argument that is both analytic and synthetic?
B. Could there be a proposition that is neither analytic nor synthetic?
3. A. What could it mean to say that an existing thing "does not exist"?
B. How could a thing be both "all black" and "all white"?
4. A. Could someone actually make the "boundless" their home?
B. What kind of logic does God use to think? (Assume God exists.)
RECOMMENDED READINGS
1. Morris Cohen, A Preface to Logic (New York: Dover Publications, 1977[1944]), Ch. One, "The Subject Matter of Formal Logic", pp.1-22.
2. Susan K. Langer, An Introduction to Symbolic Logic3 (New York: Dover Publications, 1967[1953]).
3. T.L. Heath, Introduction to The Thirteen Books of Euclid's Elements (Cambridge: Cambridge University Press, 1956), ?, "Analysis and Synthesis", pp.137-140.
4. Immanuel Kant, Critique of Pure Reason, "Introduction" (CPR 41-62).
5. Stephen Palmquist, "A Priori Knowledge in Perspective" (APK).
6. Chuang Tzu, Basic Writings, Ch.2, "Discussion on Making All Things Equal" (CTBW 31-44).
7. Dionysius the Areopagite, The Mystical Theology (MT).
8. G.W.F. Hegel, The Phenomenology of Spirit, tr. A.V. Miller (Oxford: Oxford University Press, 1977), Preface, "On Scientific Cognition", pp.1-45.
Send comments to the author: StevePq@hkbu.edu.hk
Back to the Table of Contents for this book.
Back to the listing of Steve Palmquist's published books.
Back to the main map of Steve Palmquist's web site.
border=0 height=62 width=88>