13. Mapping Analytic Relations

by Stephen Palmquist (stevepq@hkbu.edu.hk)

In the first lecture on logic we learned that logic-analytic logic, that is-abstracts from the concrete truth of a proposition, and focuses attention first and foremost on its bare (essentially mathematical) form, its truth value. This week I want to explore some ways of converting this bare form into a richer, pictorial form.

Philosophers since Aristotle, and even before that, have almost universally recognized that logic and mathematics are closely related disciplines. Until the middle of the nineteenth century, most philosophers would have said this relationship is confined primarily to arithmetic, where functions such as addition, subtraction, multiplication and division have clear analogies to logical operators such as "and", "not", etc. But then a scholar named George Boole (1815-1864) wrote a book defending what he called the "Algebra of Logic". He demonstrated that algebraic relations are also closely related in many ways to logical relations.

Although Boole's ideas are far too complex to examine in an intro?/span>ductory course, I have mentioned his discovery because I believe a similar discovery awaits us in the area of geometry. For this reason I have already been using, throughout these lectures, several simple diagrams in a way that conforms to what I call the "Geometry of Logic". This week I shall explain in detail just how these and other diagrams actually function as precise "maps" of logical relations. The first two lectures will examine ways of constructing maps that correspond to analytic and synthetic relations, respectively. Lecture 15 will then provide numerous examples of how we can use such maps to encourage and deepen our insight.

A thoroughgoing analogy can be constructed between the structure of many simple geometrical figures and the most fundamental kinds of logical distinctions, though this has rarely, if ever, been fully acknowledged in the past. The starting point of this analogy is the analytic law of identity (A=A); it posits that a thing "is what it is". To choose a diagram that can accurately represent this simplest of all logical laws, all we need to do is think of the simplest of all geometrical figures: a point. Techni-

cally, a point exists merely as a single position, with no real extension in any direction, though of course, the black spot representing a point in Figure V.1 must have some extension in order for us to see its position.

•^A Figure V.1: The Point as a Map of an Identical Relation

The function of the law of noncontradiction is to contrast the solitary "A" of the law of identity with its opposite, "-A". The geometrical figure that extends a point beyond itself in a single direction is called a line. There are, of course, two kinds of line: straight and curved. So also, there are two good ways of depicting the logical opposition between "A" and "-A" in the form of a geometrical figure: by using the two ends of a line segment, or by using the inside and outside of a circle, as shown in Figure V.2:

(a) The Circle (b) The Line

Figure V.2: Two Ways of Mapping a 1LAR

Note that I have labeled these figures with a mere "+" and "-". These symbols are derived directly from the law of noncontradiction, simply by dropping the "A" from both sides of the "+A≠-A" equation. The "A" is a formal representation for "some content", so dropping this symbol implies, quite rightly, that in the Geometry of Logic we are concerned with nothing but the bare logical form of the sets of concepts we use. Since this simple distinction arises out of the laws of analytic logic, I refer to it as a "first-level analytic relation" (or "1LAR"). As we shall see, representing this law with the simpler equation, "+ ≠ -" (i.e., positivity is not negativity), makes it much easier to work with more complex, higher levels of logical opposition.

The circle and line segment can be used as maps of virtually any distinction between two opposite terms. Such distinctions, as we learned from Chuang Tzu last week, are a commonplace in our ordinary ways of thinking about the world. We naturally divide things into pairs of opposites: male and female, day and night, hot and cold, etc. In most cases I believe the line segment offers the most appropriate way of representing such distinctions. Since the circle marks out a boundary between "outside" and "inside", we should employ this figure only when there is an imbalance between the two terms in question-as, for example, when one acts as a limitation on the other, but not vice versa.

Now if we were to stop here, the Geometry of Logic would not be a very interesting subject. No one has any trouble seeing the logical relationship between a pair of opposite terms, to say nothing of a single term in its relation to itself. Using points, line segments, or circles in such a way is helpful only when the terms in question do not define an obvious opposition. This is especially true of the circle. For example, using a circle to represent Kant's distinction between our necessary ignorance and our possible knowledge, as we did in Lecture 7 (see Figures III.5 and III.10), helped us fix in our minds the proper relationship between these two, with the former limiting the extent of the latter.

In any case, one of the most interesting and useful tools in the Geometry of Logic arises out of the simple application of the law of noncontradiction to itself. By this I am referring to cases involving each side of a pair of opposed concepts being itself broken down into a further pair of two opposing concepts. As an example, let's consider the familiar concept "one day". We all know how to perform the simple analytic process whereby we divide "one day" into two more or less equal and opposite halves, called "daytime" and "nighttime" (i.e., "not daytime"). This is a good example of a typical 1LAR. However, as with most 1LARs, if we try to apply this strict division to every moment in a day, we find there are certain times during the day when we hesitate to say whether it is "daytime" or "nighttime"; and as a result, we make a further analytic division, between "dusk" and "dawn".

In order to translate this into the form of our logical apparatus, using "+" and "-" combinations to replace the actual content of our distinctions, all we need to do is add another "+" and "-" term, in turn, to each of the original terms from the simple 1LAR. This gives rise to the following four "components" (i.e., combinations of one or more +/- terms) of a "second-level analytic relation" (or "2LAR"):

-- +- -+ ++

I call the first and last components (i.e., "--" and "++") pure, because both terms are the same, whereas I call the middle two components (i.e., "+-" and "-+") mixed, because they both combine one "+" and one "-".

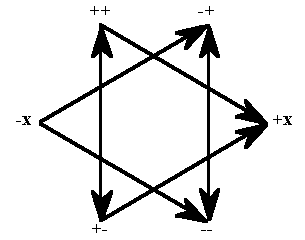
If one pair of opposites is represented by a single line segment, then two can best be represented by a combination of two line segments. As we have seen on numerous occasions already, the four end points of a cross can serve as a simple and balanced way of representing such a four-fold relation. But the same 2LAR can also be represented by the four corners of a square (cf. Figure II.3). I map the four components onto the cross and the square in the following ways:

(a) The Cross (b) The Square

Figure V.3: Two Ways of Mapping a 2LAR

The position of the four components and the direction of the arrows on each of these maps is, in a sense, arbitrary. In other words, the same components could be arranged in a number of different ways and still represent a 2LAR just as accurately. However, after experimenting with all the different ways of constructing such maps, I have come to the conclusion that these two examples represent the most common and appropriate patterns. Moreover, the above maps both follow a fixed set of rules that can help us avoid confusion and inconsistency in constructing our maps-though they may not be any better than some alternative set of rules. The rules I have chosen are, quite simply: (1) a "+" component is placed above and/or to the left of a "-" component whenever possible, giving priority to the term(s) that come first in each component; (2) an arrow between two components with the same term in the first position points away from the pure component; (3) an arrow between two components with different terms in the first position points toward the pure component; and (4) an arrow between two components that each contain only one term (i.e., the simple opposites "+" and "-") should be double-headed, to depict the tension or balance between them.

The components are mapped onto the cross in Figure V.3a according to their complementary opposites. That means the two components located at opposite ends of each line segment will share one common term. For example, the first term in both components might be a "+", while the second term will be a "+" on one side and a "-" on the other. By contrast, the components mapped onto the square in Figure V.3b are organized according to contradictory opposites. That means the component at any given corner of the square does not overlap at all with the component at the opposite corner. For example, if the component at one corner has a "+" in the first position, the component at the opposite corner must have a "-" in that position; and likewise for the second position.

The square is, in fact, the one geometrical figure that can be found fairly consistently in most logic textbooks. For it is the formal basis of what is commonly referred to as "the square of opposition". This square has proved to be very helpful in clarifying for logicians the formal relations between propositions that are opposed to each other in different ways (namely, as "contradictions" or as "contraries"). However, I do not wish to dwell on that well-known application here. Instead, since I've already used the cross as a map on numerous occasions in these lectures, let's look more closely at how it can represent the relationships between complementary opposites.

The cross enables us to visualize four distinct types of "first-level" logical relationships (i.e., simple +/- oppositions) between such sets of four opposing concepts. The first two can be called "primary" types. The first is represented by the first term in each component; as we can see in Figure V.3a, it is the same on both ends of each axis of the cross. So the first term in each component actually labels the axis itself: the vertical axis can therefore be called the "+" axis, and the horizontal axis can be called the "-" axis. The second type is represented by the second term in each component, and denotes the opposition between the two ends of any given axis. So the second term in each component mapped onto the 2LAR cross represents a "polar" (i.e., complementary) opposition-an opposition between two concepts that also share something in common. The common factor is represented by the first term of both components on a given axis of the cross: + for the vertical and - for the horizontal.

The third and fourth types of first-level relationships visible on the cross can be called "subordinate" types, because they are not as evident as the two "primary" types. Hence, when we want to call attention to them, it is helpful to draw a diagonal line through the center of the cross, either from the top right to the bottom left, or from the top left to the bottom right. The former diagonal line, as shown in Figures I.1, III.3, and IV.5, calls our attention to the secondary complementary relationship existing between the components with different first terms, but the same second term (i.e., between "--" and "+-", and between "-+" and "++"). The latter diagonal line highlights the fourth type of first-level relationship, between pairs of contradictory opposites (i.e., between the two pure components, "++" and "--", and between the two mixed components, "+-" and "-+"). I have not included this type of diagonal line in the maps used so far, but it would be appropriate to add it to the cross any time we want to call special attention to the two pairs of concepts that are diametrically opposed in a given 2LAR.

Understanding the complex web of logical relationships that exists within any set of concepts composing a 2LAR helps us see that the cross cannot properly be used to map the relationship between any randomly chosen set of four concepts. Or at least, if we use it in this way, we may not be using the cross to represent the logical form of a 2LAR. In that case the cross will only be, at best, a nice picture, and at worst, a misleading over-simplification. For only sets of concepts that can be shown to exhibit the set of interrelationships defined above, and representable by the four +/- components of a 2LAR, ought to be mapped onto the cross.

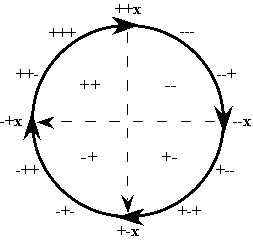
Having given this warning, I can now add that there is actually quite a simple method of testing any set of four concepts that we think might be related according to the form of a 2LAR. All we need to do is find two yes-or-no questions whose answers, when put together, give rise to simple descriptions of the four concepts we have before us. Thus, for example, in order to prove that the four concepts mentioned above, "daytime", "nighttime", "dusk", and "dawn", compose a 2LAR, all we need to do is posit the two questions: (1) Is it obviously either daytime or nighttime (as opposed to being a transition period)? and (2) Is it lighter now than at the opposite time of day? This gives rise to four possible situations, corresponding to the four components of a 2LAR as follows:

++ Yes, it is obvious, and yes, it is lighter (= "daytime")

+- Yes, it is obvious, but no, it is not lighter (= "nighttime")

-+ No, it is not obvious, but yes, it is lighter (= "dawn")

-- No, it is not obvious, and no, it is not lighter (= "dusk")

This demonstrates that the four terms in question can be mapped properly onto the 2LAR cross, as shown in Figure V.4a.

Perhaps I should also mention that we cannot produce a proper 2LAR by combining any randomly chosen pair of two questions. Or at least, we must be prepared for the possibility that in attempting to construct a 2LAR, one or more of the possible combinations of answers might end up describing a self-contradictory concept, or an impossible situation. For this reason, I use the term "perfect" to refer to a 2LAR (or any other logical relation) in which all the logically possible components also represent real possibilities. For example, consider the two questions: (1) Is it raining? and (2) Is the sun shining? At first, only three of the

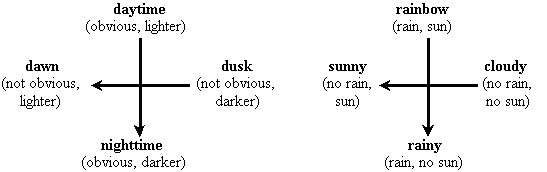
(a) Four Parts of a Day (b) Four Weather Conditions

Figure V.4: Two Examples Mapped onto the 2LAR Cross

four combinations of answers to these questions appear to depict real possibilities. If we answer "Yes" to both questions, then it might seem that we have discovered an impossible combination, since (at least here on earth) it is cloudy, not sunny, whenever it rains. If this were the case, then these two questions would compose an imperfect 2LAR. However, if we think further about this fourth option, we will realize that it does represent a real possibility. (As we shall see throughout this week, such surprises often pop up when we use the Geometry of Logic as an aid to our reflection.) For the sun does sometimes shine while it is raining: this is what is happening whenever we see a rainbow! Hence even this example, as shown in Figure V.4b, represents a perfect 2LAR, while at the same time illustrating how such maps can help us gain new insights. (Incidentally, if the second question were "Is it cloudy?", then this would be an imperfect 2LAR, since a "No" answer could not be combined with a "Yes" answer to the first question.)

Remember the map of the four elements I gave in Lecture 4 (see Figure II.4)? Now that we have analyzed the formal structure of distinctions mapped onto the cross, we can actually test that traditional set of concepts to see if it represents a perfect 2LAR. If fire is "++" and water is "--", then we would expect these to be contradictory opposites. And they are. Water puts out fire, and fire changes water into vapor. Likewise, if earth is "-+" and air is "+-", we would expect earth and air to be similarly resistant. And they are. Earth and air do not mix! What about the complementary opposites? Here we find equally appropriate results: fire needs air and earth (i.e., fuel) in order to continue burning; water can mix with air (as in soda) and with earth (as in mud). So even though the ancient Greeks had not developed the Geometry of Logic, they were intuitively able to choose, as their four basic elements, materials that correspond in real life to the form of a perfect 2LAR.

Of course, there are actually more than four physical "elements" in the universe; likewise, a day can be divided into more than just four parts, and the weather has far more than just four variations! In the same way, the process of analytic division can and does go on and on, forming increasingly complex patterns of relations between groups of concepts. In this course we have no time to examine the complex relations created by these "higher levels" of analytic division. However, I would like to mention one final example. But first I should point out that, no matter how far we go in making analytic divisions, the patterns will always follow this very simple formula:

C = 2^t

where "C" refers to the total number of different components possible and "t" refers to the number of +/- terms in each component. The latter, incidentally, is always identical to the number of the level. Thus, as we have seen, the number of divisions required to construct a 2LAR is two, the number of terms in each resulting component is also two, and the total number of components is four (2² = 4). Likewise, the number of divisions required to construct a 3LAR is three, the number of terms in each resulting component is three, and the total number of components is eight (2³ = 8).

The higher the level of analytic relation, the more complex is the map that has to be constructed to give an accurate picture of all the logical relations involved. One good example of such a complex system can be found in the ancient Chinese book of wisdom, the I Ching. This book describes a set of 64 "hexagrams" (i.e., six-part pictures), each representing some kind of life situation. The book was originally used primarily for predicting future events: in some arbitrary way, such as throwing dice, a person selects two of the 64 hexagrams, and the transformation from one to the other is then used as the basis for answering a question, usually about how some present situation will change in the future. (Thus it is also called The Book of Changes.) For our purposes, of course, the predictive power of the I Ching is not its main attraction; rather, its logical form is what interests us. For the 64 hexagrams actually function as six-term components of a 6LAR. The traditional way of representing this system of logical possibilities is to use sets of six solid or broken lines to define each hexagram. By simply replacing the solid lines with a "+" and the broken lines with a "-", we can translate this system directly into the one developed above. If we arrange the components according to their contradictory opposites (as is normally done in using the I Ching), then the intricate relationships between these hexagrams can be mapped onto a sphere, which, when projected onto a plane surface so that the opposite poles of the sphere are represented as the center and the circumference of a circle, looks like this:

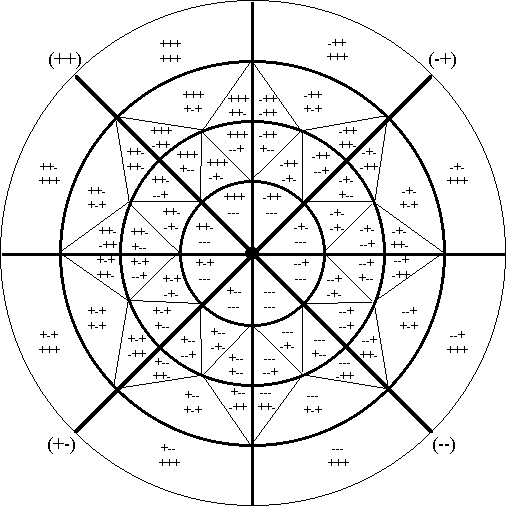
Figure V.5: A Map of the 6LAR in the I Ching

Don't worry if this map confuses you. It is intended to present the logical form of a highly complex system of concepts at a glance. If you are not familiar with the system, the map is not likely to be very meaningful. Nevertheless, I would like to end this lecture simply by pointing out that this map bears a striking resemblance to the symmetrical pictures used in some eastern religions (called "mandalas"). Such mandalas are constructed not in order to clarify the logical structure of a set of concepts, but rather, in order to stimulate new insights (and eventually, "enlightenment") in those who use them as tools for meditation (see DW 157-159). As we shall see in the next lecture, the Geometry of Logic itself is also not limited to such analytic applications, but can actually touch upon the way we live our life.

14. Mapping Synthetic Relations

In the last lecture, we saw the orderly way logical patterns are constructed when we use analytic logic in our thinking. This kind of pattern, we found, can be directly related to the patterns exhibited by some simple geometrical figures. This fact should not surprise us. For in both cases such patterns originate in the mind. Recognizing these orderly patterns, Kant suggested that reason itself contains a fixed, architectonic structure. And his promotion of what he called reason's "architectonic unity" is an inseparable aspect of his a priori approach. For his assertion that there are certain necessary conditions for the possibility of any human experience (see Lecture 8) assumes human reason operates according to a fixed order. Because reason fixes this order-this architectonic -for us, philosophers ought to do their best to understand and follow it whenever they adopt an a priori perspective in their philosophizing (i.e., whenever they ask what the mind imposes upon experience, rather than what it draws out of experience). Kant believed philosophers ought to allow these patterns to serve as an a priori "plan" for the construction of a philosophical system, much as a building contractor uses the architect's blueprints as the plan for constructing a building. It is no wonder, then, that Kant regarded Pythagoras (c.569-c.475 B.C.), not Thales, as the first genuine philosopher (see OST 392); for Pythagoras focused not on metaphysical issues, but on mathematics and number mysticism.

Logic is one kind of a priori perspective (see Figure IV.4), so we should not be surprised to find such numerical patterns playing an important role in this branch of philosophy. However, logical patterns do not relate only to our a priori ways of thinking. As Pythagoras recognized, they also relate very closely to the way we live our lives. That is one reason I ended the previous lecture with an example from Chinese philosophy. In ancient China, the I Ching was never regarded merely as a logical table of a priori thought-forms. Most-perhaps even all-who used it were not even aware of its neat, logical structure, as a perfect 6LAR. Rather, they used it intuitively, as a reflection of the ever-present changes in their daily life situations. In the real world, things do not remain eternally opposed to each other, as our concepts might lead us to believe. Instead, opposites gradually fade into each other by passing through an infinite series of degrees. Once we recognize this fact, we might wish to view the line in Figure V.2b no longer as representing an absolute separation, requiring a choice between two discrete kinds, but as representing a continuum, containing infinitely many degrees.

There is, in fact, another symbol from the Chinese tradition that performs this same, synthetic function, even though it can also serve as a map of an analytic relation. I am thinking here of the famous "Tai Chi" symbol, depicting the opposition between the forces of yin (dark) and yang (light). As shown in Figure V.6, this symbol can be regarded as simply another way of mapping a 2LAR. However, in the Chinese tradition its primary symbolic value was quite different, for it was regarded

as a pictorial expression of the fact that in real life opposite concepts, experiences, forces, etc., not only depend on each other for their own existence, but actually merge into each other through the passage of time. This is why the two halves are shaped in the form of teardrops, connoting movement. Moreover, at the very center of the large part of each "teardrop" we find the opposite force. This, like the arrow on each axis of the 2LAR cross, represents

Figure V.6: The 2LAR Implicit in the Tai Chi

the way opposites converge upon each other.

We saw in Lecture 12 that this tendency of opposites to be "the same", as Heraclitus put it, is actually the proper subject of synthetic, not analytic, logic. So I would now like to explore how to use the Geometry of Logic to construct accurate pictures of logically synthetic relations. Like analytic logic, synthetic logic also starts from a point, but the point is now regarded as already containing within itself a pair of opposites. Why? Because synthetic logic is based not on the laws of identity and non?/i>contradiction, but on the laws of nonidentity (A≠A) and contradiction (A=-A). Hence, in order to picture its extension, we must draw a line not in one direction, (from A to -A), but in two (from x to A and -A simultaneously). Thus the geometrical figure best representing this "simple" or "first-level" synthetic relation (abbreviated "1LSR") is a triangle. This threefold process can refer either to the original synthetic division of a nonidentical point into two opposites or to the synthetic integration of two opposites into a new whole (cf. Figures I.4 and I.2), as shown in Figure V.7. Ordinarily, whenever we are working with only a single triangle, it is best to use an "x" sign to represent the third term in a synthetic relation. For this third term is in a sense an "unknown" that arises out of the two "known" terms, "+" and "-", preserving what is essential in each, yet going beyond them both. However, when these two

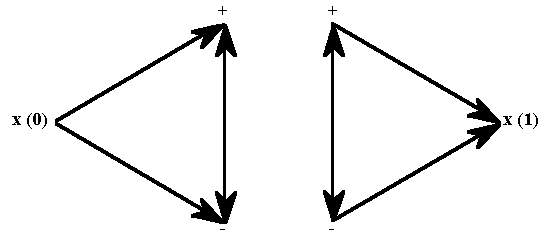
(a) The Original Synthesis (b) The Final Synthesis

Figure V.7: The Triangle as a Map of a 1LSR

types of synthetic triangle are pictured together (cf. Figures III.2 and V.7), the best way to depict the overall logical form is to label the original synthetic term with a "0", to represent its function as the common source of the two opposites, while labeling the concluding synthetic term with a "1", to represent its function as the final reunification of the two estranged opposites.

Another way of mapping a 1LSR is to use the circle given in Figure V.2a, labeling the circumference with an "x". This is appropriate because the boundary participates in both the outside and the inside of the circle, just as "x" participates in both "+" and "-". Whenever we use a circle as a logical map, the concept labeling the circumference ought therefore to fulfill a synthetic function in relation to the two opposite concepts it separates. However, synthetic logic, like analytic logic, also has higher levels of relations; and the triangle has a more natural application to these higher relations than the circle, so I'll treat the former as the standard 1LSR map.

The second level of synthetic relation (2SLR) can be constructed by regarding each of the three terms, "+", "-", and "x", as generating its own synthetic relation. This gives rise to the nine components of a 2SLR:

++ -+ x+

+- -- x-

+x -x xx

A good map for a 2SLR is a nine-pointed star, composed of a set of three intersecting triangles, though there are other possibilities as well. For our present purposes, we need not go into the details of these higher-level synthetic relations. Instead, it will be enough merely to point out that the formula governing the patterns that will appear on each level is:

C = 3^t

where "C" refers once again to the total number of different components possible and "t" refers both to the number of different terms and to the number of the level. I hope you will experiment with some of these higher levels on your own.

Mapping the regularity of higher-level logical relations, as illustrated in Figure V.5, is more appropriate to analytic relations than to synthetic relations. This is because analytic relations are produced by dividing wholes into discreet parts, whereas synthetic relations are produced by integrating parts to produce larger wholes. Because these new wholes combine opposites together in typically mysterious ways, the higher-levels tend to produce complex networks of relations that appear to be chaotic. Instead of mapping an example of such a higher-level synthetic relation here, I shall therefore discuss how synthetic logic can shed new light on one of the most interesting developments in science during the last quarter of the twentieth century. "Chaos Theory", also called "non-linear dynamics", is a rather surprising new area of mathematical physics that has great potential to explain some of the most mysterious aspects of human life. The theory claims, in a nutshell, that order comes out of chaos: when we observe whole systems, the parts seem to have haphazard relations with each other, yet on lower levels, the same system can exhibit a high degree of order. The typical illustration of the long-range effect chaos can have on the world is the claim that "the flapping of a butterfly's wings in New York may cause the weather to change in Hong Kong". How can this be true, when there is no observable cause-and-effect relation between the two? I believe the answer lies in regarding chaos as a higher-level synthetic relation. In this case, the "cause" being referred to here must not be interpreted as an ordinary cause of the sort that can be understood through analytic logic. Rather, it is like the mutual interaction between a huge collection of interwoven 1LSR triangles, whose combined syntheses are not subject to precise analysis.

A good reason for not spending more time examining higher-level synthetic relations is that the 1LSR has another application that is easier to map and so also, more useful to philosophy. For, just as we saw in Lecture 11 that analysis and synthesis are best regarded as complementary functions, so also analytic and synthetic logic have their most profound applications in the Geometry of Logic when they are joined together in a single map. The simplest way of doing this is to combine a 1LAR with a 1LSR, by putting together two intersecting triangles to form

a "star of David". The six components (2x3 = 6) of the resulting "sixfold compound relation" (or "6CR") can be placed on such a map in the manner shown in Figure V.8, with the first term in each component representing the analytic opposition between the two triangles. This figure can be constructed by sliding together the two triangles in Figure V.7, then rotating the entire figure counter-clockwise by 30? The 0 and 1 vertices become the -x and +x, respectively.

Figure V.8: The Star of David as a 6CR

This map can be used to explore the logical relationships between any two sets of three concepts we believe might be related in this way. For example, one of my students once came up with the idea of comparing the famous philosophical triad, "truth, goodness, and beauty" with the famous religious triad, "faith, hope, and love". The way to test whether or not these six concepts make up a legitimate 6CR is to find a way of mapping them onto the diagram in Figure V.8, such that the concepts placed in opposition to each other really do have characteristics that make them complementary opposites. We could begin this task by associating the "-" triangle with the philosophical concepts and the "+" triangle with the religious concepts, thus defining the basic 1LAR. But once again, I prefer to let you experiment for yourself with the other details, or with other examples of your own making.

Another way of integrating analytic and synthetic relations is to combine the simple 1LSR with a 2LAR. The twelve components (3x4 = 12) of the resulting "twelvefold compound relation" (or "12CR") can, of course, be mapped onto a twelve-pointed star; but I think a better way is simply to map them onto a circle, especially since the map then resembles the familiar figure of the face of a clock. In addition, by using a circle, we can leave the center open, to be filled in with whatever figure represents the specific set of logical relations we wish to highlight among the many that exist between the twelve components. For example, in Figure V.9, I have placed a cross inside the circle, thus dividing it into its four

main (2LAR) quadrants. However, we could also use a line, a triangle, a square, or combinations of these, to highlight other logical relations implicit within this map. What use is a complex map like this? One obvious point is that Figure V.9 coincides exactly with the traditional signs of the zodiac, which are divided into four groups of three in exactly the same way. But even apart from the light it might shed on the rational origin of such ancient "wisdom", generally scoffed at by

Figure V.9: The Circle as a Map for a 12CR

philosophers nowadays, we can find 12CRs operating in many diverse areas of human life and thought. Why, for instance, do we divide the year into twelve months (four seasons, each with three months)? Or the day into twelve hours? It's easy to pass off such facts as merely arbitrary conventions. But perhaps they have their origin in the very structure of rational thinking! This was Kant's conviction; for, as we saw in Lecture 8, his list of twelve categories fits the same pattern of four sets of three (see Figure III.9). Furthermore, as I have argued in Kant's System of Perspectives, Kant also used the same twelvefold pattern in constructing the arguments that compose his Critical systems-indeed, this pattern is the basic form of his "architectonic plan".

Other academic disciplines have no shortage of twelvefold distinctions with exactly the same structure. A famous scientist named Maxwell, for example, discovered in the nineteenth century that there are twelve distinct forms of electromagnetic forces, and that they can be grouped into four sets of three types. More recently, quantum physicists have discovered exactly twelve different types of "quarks", the basic building block of matter. Numerous examples like these could be cited. But a detailed explanation of how such applications of the 12CR actually operate is beyond the scope of this introductory course. Instead, we shall turn our attention in the next lecture back to synthetic logic itself, in order to gain a better understanding of how it operates and of how the Geometry of Logic facilitates the process of having new insights by providing visual representations of the new perspectives synthetic logic provides.

15. Mapping Insights onto New Perspectives

The main function of synthetic logic is to shock us into seeing new perspectives. Once we realize this, it becomes easier to understand how it is possible for a proposition to be meaningful even though it breaks the law of noncontradiction. The explanation is that such propositions do not actually break Aristotle's law in its strictest sense. Aristotle himself recognized that "A" could be identical with "-A" if the "A" in question is being viewed from two different perspectives. That is why in defining this law he added "at the same time, in the same respect" to the words "A thing cannot both be and not be". Things change in time, and they can be described differently when looked at in different ways, so in these cases the A≠-A law does not hold. But most of us find it quite difficult to look at a familiar subject in a new way. What synthetic logic does is to bring us face to face with an exceptional way of thinking about or looking at a familiar subject; and in so doing, it fires our imagination with insight.

This is where synthetic logic and the Geometry of Logic share a common function. For both are instrumental in providing us with the means to develop our capacity to see old issues in new ways, and in so doing, to deepen our insight into whatever is perplexing us. Indeed, taken together, these two logical tools probably constitute philosophy's most useful practical application. For as we shall see, a clear understanding of these tools can assist you in thinking and writing more clearly and more insightfully in virtually any area, not just when dealing with philosophical issues. Let us therefore look first at synthetic logic on its own, and then move from there into a discussion of how geometrical maps can be used in a similar way to promote clarity and insight.

Synthetic logic has, in fact, already been used by some philosophers to show how new insights come about. For instance, the perplexing contradictions of Chuang Tzu and the string of negations proposed by Pseudo-Dionysius (see Lecture 12) can be regarded as a way of prodding the reader to discover new insights about "the Way" or about "God", respectively. Likewise, this is the most fruitful way of interpreting Hegel's famous "dialectical" logic (see Figure IV.7): his idea that changes occur in human history whenever two opposite forces clash and give rise to a new reality, called the "synthesis", is best regarded as a description of the process whereby human perspectives change. And whenever our perspective changes, a new insight normally accompanies the change. But unfortunately, Hegel's language is so complex, and his arguments so difficult to follow, that many people end up with more confusion than insight after reading one of his books. So a better approach for our purposes will be to look at a contemporary scholar who has developed some ways of applying synthetic logic on a very down-to-earth level.

Edward de Bono (1933-) is not so much a professional philosopher as an educator par excellence. Nevertheless, some of the principles he discusses in his many books are closely related to various philosophical concerns, especially in the area of logic. For his main concern is to teach people how to think creatively. In the process of doing so, he demonstrates that the laws of synthetic logic are not just abstract principles that are difficult or impossible to apply, but are effective tools that can be used to help us solve many different sorts of real-life problems. In his book, The Use of Lateral Thinking, for example, de Bono uses geometrical terms to distinguish between our ordinary, "horizontal" way of thinking and the "lateral" thinking that always seeks to look at old situations from new perspectives. (Obviously, the former corresponds to analytic logic and the latter to synthetic logic, though de Bono does not use these terms.) He suggests that whenever we have the feeling we are "stuck" with a problem we cannot solve, the reason is not that there is no solution in sight, but that our perspective is too narrow. That is why it often helps in such situations to take a short break from our efforts: when we return, we are more likely to feel free to change the way we are looking at the problem; and often we discover that the solution was right under our nose all along!

Let me illustrate lateral thinking with a personal story. When I was a boy I used to have a great deal of trouble eating chicken with a fork and knife. I always preferred to use my fingers. When I noticed one day how easily my grandfather ate chicken with a fork and knife, I asked him how he performed this difficult task with such ease. His answer was simple: "You are trying to remove the chicken from the bone; what you need to do is to remove the bone from the chicken." This is lateral thinking! And it worked: all along the bones had been disturbing my enjoyment of one of my favorite foods; but when I changed the way I thought about my task, the disturbance virtually vanished! It is also an example of using synthetic logic, because my grandfather's suggestion enabled me to pass beyond what seemed before like an absolute opposition between "It is easy to get the chicken off the bone when I use my fingers" and "It is difficult to get the chicken off the bone when I use a fork and knife". The new perspective, "remove the bone from the chicken" enabled me to synthesize the "It is easy" of the first proposition with the "use a fork and knife" of the second proposition. Lateral thinking always cuts across our former way of thinking in just this way, much as the vertical axis of a cross cuts across the horizontal axis.

In another book, called Po: Beyond Yes and No, de Bono suggests another tool for making new discoveries. As the very title reveals, this new tool is rooted in synthetic logic even more obviously than lateral thinking. In this book de Bono coins a new word, "po", as a way of responding to questions whose proper answer is neither "yes" nor "no" (or both "yes" and "no"). The letters "P-O", he POints out, are found together in many words that play an imPOrtant role in creative thinking, such as "hyPOthesis", "POetry", "POssibility", "POtential", "POsitive thinking", and "supPOse". "PO" can also be regarded as an acronym, an abbreviation of the phrase "Presuppose the Opposite". In order to show how this new word can actually help us develop our ability to gain new insights-i.e., to see new POssibilities, new opPOrtunities, just over the horizon of our present perspective-de Bono suggests we experiment with various "po situations". To perform such an experiment, we must use "po" as an adjective, modifying a word we wish to think about creatively; but our description of the characteristics of that word must then presuppose the opposite of whatever we normally think about the objects, activities, or situations related to the word. If we think about how things would be different if this po situation were really the case, de Bono assures us that gaining new insights will become much easier.

Let's give this kind of experiment a try. Imagine I am dissatisfied with my teaching method, and I want to think of some new, creative way of teaching my classes. In order to treat this as a po situation, I must say to myself "Po teachers are ...", and complete the sentence with something that is usually not true about real life teachers. What shall we say? How about: "Po teachers know less than their students." This is just a random choice of one among many of the characteristics of the student-teacher relationship. But we do normally assume that teachers know more than their students, so the above statement, by intentionally contradicting this common assumption, can serve as a good example of a po situation. What would happen if students really did know more than their students? Well, for one thing, if I were assigned the task of teaching in such a situation, I would approach my task with humility (if not with fear and trembling!), knowing that I would probably be learning much more than my students. As a result I would certainly need to respect my students, and the common expectation that students ought to look up to me as their teacher would not be so obviously justified. Moreover, I would try to encourage students themselves to talk more, either by asking them questions in class, by having them ask me questions, or by dividing them into groups and having them talk with each other. For, since po students know best what the subject is all about, a po teacher would be very foolish not to give them ample opportunity to share what they know.

If I now step back from this po situation, and re-enter the "real world", I find I have stumbled upon several new ideas about how I can improve my teaching: I should be humble enough to learn from my students, respect them as equals in the adventure of learning, not be upset if they show some disrespect toward me, encourage them to ask and answer questions, and give them opportunities to discuss issues among themselves. The first time I gave this lecture, I had not prepared these insights beforehand: they just came to me as I was experimenting with de Bono's method in front of the class. Yet I think these are really very good insights, don't you? If so, it is important to remember that they did not come to me because I am especially clever; they came because I used po to think laterally, thus leading me to adopt a surprising new perspective on a familiar subject. You can prove this for yourself simply by using the same method to reflect on any area you wish to improve or any topic you need to view with fresh insight. Just remember: po thinking stimulates insights because it causes us intentionally to adopt a perspective we know is contradictory to the real situation-a practical application of synthetic logic if ever there was one!

I hope the foregoing examples have helped you see the great value -indeed, the necessity-of using synthetic logic. I'm confident that they have, because over the years I've noticed that beginning philosophy students often find it easier to grasp synthetic logic than do professional philosophers! This, no doubt, is partly because western philosophers are often taught to have a prejudice in favor of the exclusive validity of analytic logic. In some traditions logic is defined as "analysis"; so of course, anyone who tries to propose a nonanalytic logic is regarded as speaking nonsense! Nevertheless, as we have seen, synthetic logic exhibits patterns just as much as analytic logic; so if we define logic as "patterns of words", then synthetic and analytic logic clearly ought to have an equal right to be called "logic". (Philosophers trained in eastern ways of thinking, incidentally, sometimes develop a prejudice in favor of synthetic logic; in the end this is no better than the western prejudice. A "good" philosopher will be able to appreciate the value of using both.) Perhaps another reason beginners can accept synthetic logic so easily is that it actually requires less formal training to use synthetic logic than analytic logic: whereas analytic logic is the logic of knowledge (especially thinking), synthetic logic is the logic of experience (especially intuiting). In this sense, we can call synthetic logic the logic of life.

If you are reading this as a student, your life is likely to be focused largely on studying, writing papers, and taking tests. With this in mind, I shall devote the rest of this lecture to suggesting how an awareness of perspectives can be an aid to improving your writing skills-a topic that should interest all readers, especially those writing insight papers. We have already seen that insights tend to arise when we learn to shift our perspective (as in lateral and po thinking) and that synthetic logic is the logic that governs such changes; we shall now proceed to examine how an ability to map our perspectives according to the principles of the Geometry of Logic can improve our receptivity to insight still further.

First, let me warn you that before you actually use a logical map in a paper or essay, you should carefully assess whether the reader(s) will be receptive to thinking in pictures. Some people have a natural preference for this type of thinking, while others seem to be virtually incapable of understanding it. My own doctoral dissertation at Oxford was initially rejected because one of my examiners had an allergic reaction to my use of diagrams. He claimed my thesis contained "publishable material", but not as long as it was filled with diagrams based on the Geometry of Logic. Ironically, the chapter where I defended my use of diagrams (Chapter III of KSP) had at that time already been accepted for publication in a very reputable professional journal! Nevertheless, I had to rewrite my dissertation, removing the diagrams, before it was deemed acceptable by that examiner. This illustrates that a person's response to a diagram may have more to do with his or her bias (e.g., an unquestioned myth about what an academic thesis should look like) than with any rationally justifiable objection to pictorial thinking. If you think your reader(s) might have such a bias, you can still use diagrams to help organize your thinking and stimulate insights; but it would be wise not to include your diagrams in the final version of your essay. But if your teacher likes using diagrams or at least has an open mind about such things, including the actual diagram can be an impressive way of making a good essay even better.

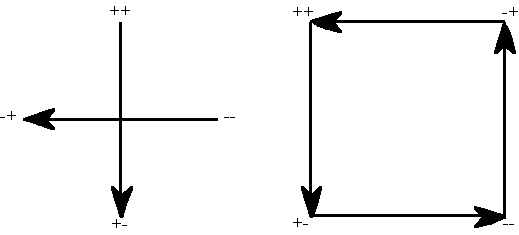
The most basic use for a logical map is in outlining the overall flow of your essay, just as I did for this book in Figure I.1. What you may not have noticed is that the 2LAR map provides a pattern that can serve as a universal guide for constructing a clear and complete argument. In its simplest application, as shown in Figure V.10, the pure components (-- and ++) stand for the Introductory and Concluding parts

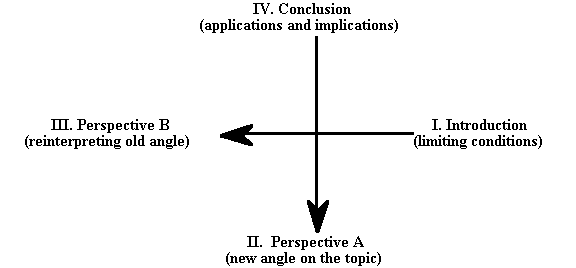
Figure V.10: The Four Parts of an Organized Essay

of your essay. In a well-organized essay these will not be mere "before and after" summaries of what is contained in the other parts. Rather, a good introduction sketches out the basic limiting conditions on the topic, just as "recognition of ignorance" did for this course. Likewise, a good conclusion leaves the reader with clear and interesting practical applications and/or ideas for future research. As we shall see in Part Four, the "wonder of silence" will do just that for our study of philosophy. The impure components (+- and -+), by contrast, will present two opposite perspectives on the topic at hand. In our case, thinking (logic) and doing (wisdom) are the two opposites that occupy our attention in Parts Two and Three. Viewing these opposites as two perspectives can lead to an especially insightful essay in cases where the views examined in these two parts tend to be regarded as competing theories or approaches. If you can effectively demonstrate how the two are actually compatible and/or give a clear account of why certain incompatibilities are unavoidable, you will be well on your way to writing an impressive piece.

Having a predetermined plan for the format of what you intend to write may seem at first like an illegitimate procedure: since the real world is not so neatly divided, how can we know in advance whether the topic will actually fit into such a neat, logical pattern? Kant would reply that such a question ignores the fact that reason itself has an essentially architectonic nature. That is, our thinking is (or ought to be!) orderly and patterned, so in any essay that involves rational thinking, that order ought not to be left to chance. Of course, the content of any essay cannot be predetermined in this way. But if the essay is one that can benefit by being written in a clear and orderly way, then selecting a pattern as common as the 2LAR will virtually guarantee an increase in its level of clarity and persuasiveness. Some essays may be so detailed that they will require a more complex pattern, such as the 12CR used in organizing this course (and its sequel, DW, as well as KSP and KCR). The alternative approach, adopted by most writers even of highly abstract philosophical essays, is simply to divide the essay into a haphazard number of sections without following any rule. Yet this leaves the reader totally clueless as to why the essay is divided up in just this way, and not some other.

By far the greatest benefit that comes from using the Geometry of Logic to pre-plan a piece of writing is that doing so calls attention to gaps and previously undetected connections between the various themes being considered. In the first two lectures this week, I gave several examples of how geometrical maps can be used to help promote insights. (Remember the rainbow?) The potential for giving other such examples is so great that I could easily fill a whole book with them! But for our purposes it will be enough to provide one more example to illustrate how a map can assist us in deepening our insight by discovering a new perspective on an old, familiar topic.

When I was preparing the present edition of this book, I had taught Introduction to Philosophy more than thirty times, always using something like Figures I.1 and I.3 on the first day as a preview of what students could expect. Then one day after a Philosophy Cafe meeting here in Hong Kong, I was discussing the nature of silence with one of the participants. Suddenly as I spoke I realized that Parts Two and Four of this course can be described as the two ways human beings experience meaning. The word "meaning" can therefore label the vertical pole on Figure I.3. As I went home that night, this image of the labeled vertical pole caused me to wonder: How, then, should the horizontal pole be labeled? Had I not organized this course using the Geometry of Logic, this question would surely never have arisen. But it now became so obvious that I was amazed I had never in 13 years thought of this issue! For several weeks I reflected on this matter without coming up with an answer. Then, in a conversation with a former student, I finally sat down and drew the diagram. Seeing the horizontal pole with "ignorance" on one end and "knowledge" on the other stimulated me all in a flash to think of two good answers: Parts One and Three both deal with reality, but from two different perspectives (ultimate and non-ultimate); but a more natural way of contrasting this with "meaning" is to refer to it as "existence". My new insight was now complete: the overall aim of this course is to share a vision of what it means to exist.

QUESTIONS FOR FURTHER THOUGHT/DIALOGUE

1. A. How would you map a compound relation higher than a 12CR?

B. Could there be a half-level of analytic division (e.g., a 1¹/₂LAR)?

2. A. Could a cross be used to map a synthetic relation?

B. Could a triangle be used to map an analytic relation?

3. A. Could "x" and "+" (or "x" and "-") be synthesized?

B. Are there really any magic numbers?

4. A. What would po lateral thinking be like?

B. Is it possible to have an insight that could never be mapped?

RECOMMENDED READINGS

1. George Boole, An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities (London: Dover Publications, 1854).

2. Stephen Palmquist, Kant's System of Perspectives, Ch. III, "The Architectonic Form of Kant's Copernican System" (KSP 67-103).

3. Stephen Palmquist, The Geometry of Logic (unpublished; working draft available at http://www.hkbu.edu.hk/~ppp/gl/toc.html).

4. Underwood Dudley, Numerology: Or, what Pythagoras wrought (Washington D.C.: The Mathematical Association of America, 1997), Ch.2, "Pythagoras", pp.5-16.

5. Robert Lawlor, Sacred Geometry: Philosophy and practice (London: Thames and Hudson, 1982).

6. Edward de Bono, The Use of Lateral Thinking (Harmondsworth, Middlesex: Penguin Books, 1967).

7. Edward de Bono, Po: Beyond yes and no (Harmondsworth, Middlesex: Penguin Books, 1972).

8. Jonathan W. Schooler, Marte Fallshore, and Stephen M. Fiore, "Putting Insight into Perspective", Epilogue in R.J. Sternberg and J.E. Davidson (ed.), The Nature of Insight (Cambridge, Mass.: MIT Press, 1995), pp.559-587.

---

Send comments to the author: StevePq@hkbu.edu.hk

Back to the Table of Contents for this book.

Back to the listing of Steve Palmquist's published books.

Back to the main map of Steve Palmquist's web site.

border=0 height=62 width=88>